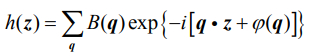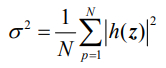-
0 前言
-
精密仪器的应用推动了机械零部件的纳米化,相应的接触界面研究已从微米尺度扩展至纳米尺度。在微纳尺度下,接触界面表现为若干高度、曲率不同的粗糙峰[1-2]。在外加负载作用下,粗糙峰的存在导致界面实际接触面积远小于几何名义面积,会引起局部应力集中并可能导致机械零部件屈服或失效。因此,有必要分析纳米级粗糙界面的法向接触行为,揭示粗糙界面在外加负载作用下,法向接触力、实际接触面积、界面等效变形量等关键参量的变化特性,为改善精密仪器的界面特性提供理论参考。
-
机械零部件间的接触实质为粗糙峰间的相互挤压变形,建立粗糙界面的等效力学模型是揭示整个接触界面变形机理的前提。相关研究者对微米尺度的粗糙界面接触过程展开研究,例如,黄文强等[3] 阐述了在真空环境下,粗糙界面的实际接触面积会随着外加负载的增大而增大。李炎等[4]分析了表面形貌对二维平面线接触模型的影响,提出一种计算粗糙表面接触应力分布的数值模型。王悦昶等[5]根据表面形貌特征梳理不同粗糙表面仿真方法的原理、算法和优缺点,阐明了粗糙表面仿真的前景。闫铎等[6]提出一种新型粗糙表面层级接触模型,实现粗糙表面的弹性接触响应的准确预测,显著降低多尺度粗糙表面接触力学建模的计算规模。 JACKSON 等[7]考虑了材料屈服应力的影响,建立弹塑性半球与刚性平面接触的有限元模型,揭示接触体的几何形状对塑性变形区域应力的影响。LIU 等[8]利用有限元分析正弦曲面与刚性平面之间的塑性接触过程,揭示正弦曲面曲率的非均匀变化会导致赫兹接触理论无法用于初始塑性变形阶段。 MEGALINGAM 等[9]构建微米级粗糙界面法向接触的有限元模型,推导了在弹性、弹塑性和塑性状态下接触载荷与接触面积之间的经验表达式。然而,无论是有限元法还是试验方法都局限于研究微米尺度粗糙界面的接触过程,难以用于纳米级粗糙界面接触特性分析。
-
随着计算机技术的不断发展,分子动力学方法广泛应用于纳米尺度的界面接触分析。LUAN 等[10-11]通过单粗糙峰粘附接触的分子动力学模拟揭示是原子离散性导致连续介质力学理论在原子尺度的不适用。雷海东等[12]模拟了刚性分形粗糙峰与弹性平面的粘附接触过程,研究表明在趋近阶段,粘附力和载荷-位移曲线均受到粗糙峰表面形貌的影响。林起崟等[13]阐明了多晶铜基体的最大法向接触力随晶粒尺寸的减小呈先增后减的趋势。HE 等[14] 通过纳米级粗糙峰间法向接触的分子动力学模拟揭示金属摩擦接触的本质为原子扩散。SI 等[15]模拟了纳米尺度下粗糙峰与光滑平面之间的粘附接触行为,阐明在纳米尺度下粘附会对摩擦力产生显著影响。上述研究将纳米级粗糙界面简化为单个或多个规则的粗糙峰接触,该简化方式可能会导致部分接触界面形貌信息的丧失,因此,建立与实际情况更相符的粗糙界面接触模型至关重要。ZHENG 等[16-17] 构建了纳米级粗糙界面润滑接触的分子动力学模型,探究粗糙度和润滑因素对界面接触特性的影响规律,揭示了纳米级粗糙界面发生接触变形上受润滑作用的影响。黄健萌等[18]和 DAI 等[19]研究了纳米级粗糙表面与刚性基体之间的法向接触过程,其研究表明:在纳米尺度下,实际接触面积与法向接触力之间仍然存在线性关系,且该线性关系受到界面变形程度的影响。黄仕平等[20-21]采用分子动力学格林函数法模拟纳米级粗糙界面接触过程,揭示了多粗糙峰界面的接触和摩擦特性,阐明纳米尺度数值计算结果和经典力学模型的差异性。SPIJKER 等[22-23]研究滑动速率、表面粗糙度和法向负载对纳米级粗糙界面的滑动干摩擦影响,揭示了在纳米尺度下粗糙峰的接触变形会使接触界面愈加光滑。综上所述,目前关于纳米级粗糙表面形貌与接触参量的映射关系研究相对较为有限,仍未揭示不同外加负载下粗糙界面接触参量的动态变化特性。
-
本文结合表面功率谱密度函数和分子动力学方法,构建纳米级粗糙铜-金刚石界面法向动态接触模型,研究粗糙界面法向接触力、实际接触面积和等效变形量等关键接触参量的变化特性,分析外加负载、表面粗糙度等因素对界面法向接触力学特性的影响规律,构造纳米级粗糙界面等效变形量与实际接触面积间的经验公式,为微纳尺度的界面接触研究提供理论参考。
-
1 纳米级粗糙界面法向接触分子动力学模型
-
1.1 纳米级粗糙表面建模
-
式中,z =(x,y)为二维矢量,表征粗糙表面的不同几何位置,h(z)表示粗糙表面轮廓的高度分布,q 表示包含分量 2π / L 的所有波矢量,i 表示虚数单位,B(q)表示波矢量振幅,φ(q)表示相互独立的随机相位,L 表示纳米级粗糙表面的取样长度,其取值参考所构建模型的尺寸,此处 L = 8.92 nm。根据式(1),得到粗糙表面轮廓高度的功率谱密度函数,其表达式为:
-
式中,C(q)表示表面轮廓高度的功率谱密度函数,初始基准平面高度为 h(0)= 0,<···>表示集合均值,即对具有相同统计特性的粗糙峰高度集合进行平均。当波矢量 q 采样密度足够大时,离散粗糙峰连接形成连续轮廓,则粗糙表面功谱密度函数 C(q)可表示为:
-
式中,A 表示取样截面面积,由于 x 方向和 y 方向的取样长度一致,故 A = L2。根据表面均方根粗糙度 σ 定义得到其表达式为:
-
式中,p 表示第 p 个取样点,N 表示采样点总数。根据能量守恒定律,结合式(2)~(4),得到均方根粗糙度 σ 与表面轮廓高度的功率谱密度函数 C(q)的关系表达式:
-
式中,m、n 分别表示取样截面在不同方向的采样点数,m = n = 30。将粗糙表面轮廓高度的功率谱密度函数 C(q)作径向平均,对均方根粗糙度 σ 进行赋值,采用逆傅里叶变换构建得到纳米级粗糙表面,如图1 所示。可以看出,随着均方根表面粗糙度 σ 由 0.2 nm 增大至 0.8 nm,粗糙峰的数量增多,粗糙峰偏离基准平面高度增大,意味着表面轮廓的粗糙程度加深。
-
图1 不同表面形貌的纳米级粗糙表面
-
Fig.1 Nanoscale rough surfaces with different morphologies
-
1.2 纳米级粗糙界面法向接触模拟
-
调整粗糙表面的基准平面高度,筛选基底表面轮廓原子,构建纳米级粗糙铜-金刚石界面法向动态接触的分子动力学模型,如图2 所示。图2a 为该接触模型的三维结构示意图,其基本尺寸为 8.92 nm× 8.92 nm×22.78 nm,上、下粗糙表面基准平面高度间距 d0 = 6 nm。
-
图2 铜-金刚石界面法向接触的分子动力学模型
-
Fig.2 Molecular dynamics model of normal contact at nanoscale rough Copper-Diamond interface
-
图2b 为模拟体系的条件设置示意图,该接触模型可分为上、下两部分,由外至内依次为边界层 ( Boundary)、恒温层( Thermostat)、牛顿层 (Newtonian),各模拟层高度比约为 1∶1∶5。模型上半部分为铜基体,由晶格间距为 3.615 Å、晶面为 100 的面心立方晶胞铜原子(FCC Cu)构成,包含约 61 900 个原子,选用 Embedded Atom Method (EAM)势中的 cu_u3.eam 势描述铜原子间相互作用力[26]。对铜-边界层(Cu-Boundary)作刚性处理,保证均匀受载且不发生变形。模型下半部分为金刚石基体,由晶格间距为 3.657Å、晶面为[100]的金刚石立方晶胞碳(Diamond C)原子组成,包含约 125 200 个原子,碳原子间的相互作用力选用SiC.teroff 势描述[27]。碳-边界层(C-Boundary)作固定处理,防止法向加载过程中模型整体发生偏移。法向接触模拟中,铜-牛顿层(Cu-Newtonian)与碳-牛顿层(C-Newtonian)构成纳米级粗糙铜-金刚石界面,界面原子间相互作用力选用为 Lennard-Jones(L-J)势描述,其表达式为[28]:
-
式中,U(r)表示两原子间的势,ε 表示阱深,σ 表示势能为零时的特征长度,r0 表示全局截止距离,r 表示原子间距。根据洛伦兹-贝塞洛定律确定 L-J 势参数[29-30]:
-
式中,σC-Cu 为粗界面碳与铜原子间的特征长度,σC 为碳原子间的特征长度,σCu 为铜原子间的特征长度,εC-Cu 为粗糙界面碳与铜原子间的阱深,εC 为碳原子间的阱深,εCu 为铜原子间的阱深。FILIPPOVA 等[29]计算确定了铜原子的势能参数值,σCu = 0.229 nm,εCu = 0.52 eV;RAPPÉ 等[31]计算得到碳原子的势能参数,σC = 0.385 nm,εC = 0.004 55 eV。考虑到粗糙界面存在氧化、黏附等作用,将势能参数相对于初始值减少 10%[22]。结合式(7)和式(8) 计算界面的势能参数为: εC-Cu = 0.014 648 eV, σC-Cu = 0.030 7 nm,r0 = 0.9 nm。
-
模拟的时间步长设置为 0.001 ps。为消除边界效应,须将接触界面方向(z 向)设置为自由边界条件,基体四周表面设置为周期性边条件。通过正则系综(NVT)约束模拟体系,采用 Nosé-Hoover 热浴法调节系统温度为 300 K。模拟粗糙界面接触前,需要对分子动力学模型进行充分弛豫以保证系统稳定。弛豫阶段持续 40 ps,在原子热运动的影响下,表面粗糙度略有降低。然而,该细微变化对粗糙界面接触特性的影响可以忽略不计[32]。充分弛豫后,法向接触过程中选用微则正系综(NVE)约束模拟体系,采用速度标定法将恒温层(Thermostat) 温度控制为 300 K,在铜-边界层上沿 z 轴负方向均匀加载(P = 0.05、0.10、0.15、0.20、0.25 GPa)。图3a 揭示了系统温度 T 随时间 t 的变化规律,可以看出弛豫过程以及加载过程,系统温度 T 始终在 300 K 左右波动变化。图3b 反映系统能量 E 随时间 t 变化情况,系统总能 Et 与系统势能 Ep波动呈现出相同的变化趋势。因此,基于系统温度 T 和能量 E 的变化过程,表明所建立的粗糙铜-金刚石界面准静态接触模型处于热力学稳定状态。
-
图3 模拟系统温度和能量变化
-
Fig.3 Variations in temperature and energy of simulation system
-
2 纳米级粗糙界面的法向接触特性
-
2.1 法向接触力和接触应力
-
粗糙界面的接触力和接触应力都会直接影响零部件的连接可靠性。在外加负载 P 作用下,铜-金刚石界面原子间相互作用力致使接触体发生变形,由于接触体内部原子间相互作用力为内力,故以铜-牛顿层(Cu-Newtonian)与碳-牛顿层(C-Newtonian) 间相互作用力(外力)定义纳米级粗糙界面的法向接触力 FN,即统计截止距离 r0 内所有铜-牛顿层 (Cu-Newtonian)原子与碳-牛顿层(C-Newtonian) 原子相互作用合力的 z 向分量定义法向接触力 FN。持续加载接触过程中,由于原子的热效应,法向接触力 FN时刻变化,故以最大法向接触力 FN为基准分析其变化规律,误差棒对应于法向接触力 FN的标准差。不同表面形貌下法向接触力 FN随外加负载 P 的变化规律,如图4 所示。
-
图4 不同表面形貌下法向接触力 FN-外加负载 P 变化
-
Fig.4 Variations in normal contact force FN with applied load P under different surface morphologies
-
外加负载 P 恒定时,界面的法向接触力 FN 与均方根粗糙度 σ 呈负相关。法向接触力 FN与界面接触原子间相互作用力呈正相关,故承受相同外加负载 P 时,铜-金刚石界面愈加光滑,实际接触原子数量越多,表现为原子的热运动愈加剧烈,即法向接触力 FN 及其波动范围也愈大。而表面粗糙度恒定时,随着外加负载 P 由 0.05 GPa 增大至 0.25 GPa,法向接触力 FN近似线性增长,这与连续介质力学理论一致[10-11]。对比表面粗糙度 σ 为 0.2 nm 和 0.8 nm 的接触过程,可以看出,σ = 0.8 nm 对应的法向接触力 FN 受外加负载 P 的影响较小,这是由于界面接触原子数量直接影响法向接触力 FN,当界面粗糙程度较大时,接触原子数量相对越少,此时外加负载 P 影响作用减弱。
-
揭示粗糙界面接触区域的应力分布,可为避免接触体发生应力集中提供理论依据。在纳米尺度下,单粗糙峰的接触应力情况无法直接获取,依据碳原子晶格间距,将接触界面沿 x-y 平面划分为 25×25 的区域块,以表面粗糙度 σ = 0.6 nm 的接触界面为例,如图5 所示,通过平均区域块内原子间应力得到粗糙界面接触应力 σH 分布情况。随着时间 t 由 80 ps 转变至 90 ps 时,粗糙界面的接触应力 σH明显增大。
-
图5 粗糙界面接触应力 σH分布
-
Fig.5 Contact stress σH distribution of rough interface
-
粗糙峰间相互接触表现为界面接触原子间相互作用力,而原子间相互作用力实质为原子排斥力与原子吸引力的共同作用。为清晰阐明原子间的相互作用力,图6 阐明了 Lennard-Jones 势中势能与原子间作用力的关系,F(r)表示原子间的相互作用力,可以看出原子间距影响原子间相互作用力,原子排斥力和原子吸引力均与原子间距呈负相关,而原子排斥力变化速率比原子吸引力变化速率更大。接触应力 σH的正负性反映未接触区域与实际接触区域的差异性。铜-金刚石界面未发生接触时,接触体内部原子排斥力比原子吸引力更大,导致表面接触应力 σH方向与 z 轴正方向一致,即应力值为正(蓝色区域),如图5 所示。铜-金刚石界面发生接触时,界面接触原子间相互作用力主要表现为原子排斥力,界面原子排斥力远大于接触体内部原子排斥力,故界面接触应力σH方向与 z 轴负方向一致,即应力值为负(橙色区域)。表面轮廓高度分布导致各区域块内的原子数量、原子间距的不同,区域块的原子间相互作用力随之变化,即不同区域接触应力σH不同。在图5a 中,时间 t = 80 ps 时,未接触区域应力主要在 0~15 GPa 内变化,对应于图中蓝色区域。随着接触程度的加深,界面接触原子数量增多,实际接触区域随之增大,如图5b 所示,t = 90 ps 时,部分区域接触应力 σH由正转变为负,橙色区域所占比例增大。同时,界面接触原子排斥力随接触原子数量的增多而增大,故实际接触区域应力值增大;而未接触区域受邻近原子排斥力影响导致其接触应力值减小。
-
图6 Lennard-Jones 势中势能与原子间作用力的关系
-
Fig.6 Relation between potential energy and interatomic force in the Lennard-Jones (LJ) potential
-
2.2 实际接触面积
-
实际接触面积反映粗糙界面的接触程度,分析其变化规律对于揭示纳米级粗糙界面法向接触特性至关重要。与易获得接触界面轮廓的连续介质力学模型相比,分子动力学模型由离散原子构成,且原子间相互作用力的存在导致原子间存在间隙,难以直接准确定义两原子间的接触。因此,在纳米尺度下,通常根据两原子的距离阈值来定义接触。对于单晶金属材料,通常是以 0.5 nm 作为判断原子接触的阈值[33-34]。图7 为纳米级粗糙界面原子间接触示意图,若原子 i 与原子 j 间距 rij 大于 0.5 nm,则判定两原子未发生接触;反之,则判定已发生接触。
-
图7 纳米级粗糙界面原子间接触
-
Fig.7 Atomic contact at nanoscale rough interfaces
-
根据接触界面碳-牛顿层与铜-牛顿层原子间距阈值确定铜-金刚石界面发生接触的原子数量,从而得到纳米级粗糙界面的实际接触面积 Ar,如图8 所示。在外加负载 P 作用下,两个粗糙表面间距减小,部分原子开始接触,将界面接触原子投影至 x-y 平面,得到粗糙界面实际接触面积 Ar;持续加载下,接触原子数量增多,实际接触面积 Ar随之增大,由此揭示纳米级粗糙界面实际接触面积Ar的动态变化过程。
-
图8 纳米级粗糙界面的实际接触面积 Ar
-
Fig.8 Actual contact area Ar of nanoscale rough interfaces
-
粗糙界面的面积接触率 Ar / A0 为实际接触面积 Ar与名义接触面积 A0 之比。外加负载 P、均方根粗糙度σ对纳米级粗糙界面接触率Ar / A0的影响规律,如图9 所示。可以看出,表面粗糙度 σ 恒定时,面积接触率 Ar / A0 与外加负载 P 呈正相关,即外加负载 P 越大,粗糙界面的接触程度越深入,与现有文献[10]和[11]分析结论一致。外加负载 P 不变时,面积接触率 Ar / A0随表面粗糙度 σ 的增大而减小,这是因为接触界面轮廓高度分布受表面粗糙程度影响,接触界面愈加粗糙,粗糙峰偏离基准平面程度越大,构成粗糙峰的原子间距越大,实现原子间的真实接触所需要的外加载荷 P 越大。当表面粗糙度 σ 较小,如 σ = 0.2 nm 时,面积接触率 Ar / A0 波动变化较明显,这是因为纳米级粗糙界面接触本质是原子间相互作用力,而原子间相互作用力直接受原子间距影响;对于表面更加光滑的接触界面,相同负载下,上、下表面的原子间距更趋于一致,在接触界面表现为强的原子间作用力。在原子层面,强的原子间作用力必定导致原子的热运动愈加剧烈,这意味着纳米尺度下,实际接触面积 Ar是动态变化的,且该动态变化随着表面粗糙度的增加而减小。
-
图9 不同表面形貌下面积接触率 Ar / A0-外加负载 P 变化
-
Fig.9 Variations in contact area ratio Ar / A0 with applied load P under different surface morphologies
-
2.3 界面等效变形量
-
粗糙界面的接触变形量是反映接触特性的重要参数之一。由于接触界面包含若干曲率不同的粗糙峰,难以直接分析单粗糙峰的接触变形情况,故基于粗糙铜-金刚石界面的基准平面间距变化量定义界面等效变形量 u,如图10 所示。
-
图10 纳米级粗糙界面法向接触过程
-
Fig.10 Normal contact process of nanoscale rough interfaces
-
上、下粗糙表面处于未接触状态时,系统初始高度为 H0,粗糙表面基准平面高度间距 d0;随着粗糙界面开始接触,系统高度变化为 H1,两粗糙表面基准面高度间距减小至 d1;在外加负载 P 持续作用下,系统高度变化为 H2,两粗糙表面基准面高度间距为 d2。纳米级粗糙铜-金刚石界面法向接触的等效变形量 u 可定义为:
-
根据式(9),结合初始系统高度 H1,将界面接触等效变形量 u 作无量纲处理,得到无量纲等效变形量 δ 为:
-
外加负载 P、表面粗糙度 σ 对界面无量纲等效变形量 δ 的影响规律,如图11 所示。
-
图11 不同表面形貌下无量纲等效变形量 δ-外加负载 P 变化
-
Fig.11 Variations in dimensionless equivalent deformation δ with applied load P under different morphologies
-
接触界面粗糙度 σ 相同时,无量纲等效变形量 δ 与外加负载 P 正相关,这是由于在持续加载过程中界面接触原子间相互作用力,导致接触体内部原子扩散,如图12 所示。随着外加负载 P 的增大,界面接触原子间相互作用力随之增大,致使原子间相互挤压,如图12 中标注原子(蓝色)所示,接触界面等效变形量 u 随之增大。外加负载 P 相同时,表面粗糙度 σ 越大,无量纲等效变形量 δ 也越大,对于表面粗糙度 σ 较大的接触界面,粗糙峰的曲率较小且偏离基准平面的高度越大,粗糙峰的承载能力相对较弱,更易发生接触变形,无量纲等效变形量 δ 的变化反映了接触界面粗糙峰抵抗形变的能力。此外,粗糙铜-金刚石界面无量纲等效变形量 δ 呈现波动变化,图11 中通过无量纲等效变形量 δ 的标准差表征其波动变化。界面接触原子间相互作用力影响着原子热运动,而原子热运动致使恒定负载下的界面接触变形量 u 并非定值,即无量纲等效接触变形量 δ 呈现出波动变化。粗糙峰曲率与接触界面粗糙度呈负相关,曲率较小的粗糙峰包含原子数量更少,单粗糙峰内部原子间相互作用力更小,原子热运动受其影响,故相同负载下的等效变形量 δ 波动愈弱。
-
图12 外加负载 P 作用下的原子扩散
-
Fig.12 Atomic diffusion under applied load P
-
3 实际接触面积与等效变形量的映射关系
-
面积接触率 Ar / A0与无量纲等效变形量 δ 间的双对数变化关系如图13 所示,可以看出,面积接触率 Ar / A0 随等效变形量 δ 在双对数坐标 ln(Ar / A0)-ln(δ)中近似线性变化,因此,纳米级粗糙界面接触率 Ar / A0与等效变形量 δ 之间呈非线性幂律关系,且表面粗糙度 σ 是影响面积接触率 Ar / A0 与等效变形量 δ 间映射关系的重要参数。采用幂函数 Ar / A0=cδ α 拟合面积接触率 Ar / A0 与无量纲等效变形量 δ 的关系,将幂函数 Ar / A0=cδ α 取对数为:
-
图13 面积接触率 Ar / A0-无量纲等效变形量 δ 的双对数变化曲线
-
Fig.13 Double logarithm variation curves of contact area rate Ar / A0 with dimensionless equivalent deformation δ
-
基于最小二乘法进行线性回归拟合,结果如表1 所示,其中 R2 表示相关系数,反映因变量通过回归关系能被自变量解释的比例,取值范围为 0~1; 多组分子动力学模拟结果的拟合相关系数 R2 均趋近于 1。结果表明,纳米级粗糙界面实际接触面积Ar与接触变形量 u 间满足幂律关系,两者间函数映射关系式为:
-
式中,c 和 α 分别为受表面形貌影响的幂系数和幂指数。纳米尺度下,粗糙界面的实际接触面积 Ar与法向接触力 FN 间呈线性关系[35]。AKARAPU 等[36] 提出界面粗糙度变化量 hσ 与法向接触力 FN 间的关系表达式为:
-
式中,a、γ 均表示常数,E'表示粗糙界面等效模量, d 表示粗糙界面分离间距。结合式(13),得到实际接触面积 Ar 与界面粗糙度变化量 hσ 的关系为: ln(Ar / A0)~hσ。界面粗糙度变化量 hσ与等效变形量 u 呈正相关,即实际接触面积 Ar与等效变形量 u 呈幂律关系,验证了文中模拟结果的合理性。
-
4 结论
-
通过分子动力学模拟研究不同外加负载 P、表面粗糙度 σ 下纳米级界面法向接触动态过程,揭示了纳米级粗糙界面法向接触力 FN、接触应力 σH、实际接触面积 Ar、等效变形量 u 等关键参量的动态变化特性,建立实际接触面积 Ar与接触变形量 u 间的经验表达式,为微纳尺度接触界面提供理论参考,从而为优化精密仪器的界面特性提供科学依据。具体结论如下:
-
(1)当界面粗糙度 σ 恒定时,法向接触力 FN、实际接触面积 Ar、接触变形量 u 与外加负载 P 呈正相关,与微米级粗糙界面的接触特性一致。
-
(2)相同外加负载 P 下,界面粗糙度 σ 的增大导致接触原子数量的减小,法向接触力 FN、实际接触面积 Ar也随之减小。
-
(3)表面形貌影响界面原子间相互作用力,接触力 FN、实际接触面积 Ar等接触参量的波动变化随着表面粗糙度 σ 增大而减小。
-
(4)外加负载作用下,纳米级粗糙界面的实际接触面积 Ar与等效变形量 u 呈幂律关系,即等效变形量相同时,界面越粗糙,实际接触面积越小。
-
参考文献
-
[1] PROKOPOVICH P,PERNI S.Multiasperity contact adhesion model for universal asperity height and radius of curvature[J].Langmuir,2010,26(22):17028-17036.
-
[2] YU X,SUN Y Y,WU S J.Multi-stage contact model between fractal rough surfaces based on multi-scale asperity deformation[J].Applied Mathematical Modelling,2022,109:229-250.
-
[3] 黄文强,占旺龙,黄平.外界压力对粗糙表面摩擦与接触的影响研究[J].机械工程学报,2019,55(21):81-87.HUANG Wenqiang,ZHAN Wanglong,HUANG Ping.Study on effect of external pressure on friction and contact of rough surfaces[J].Journal of Mechanical Engineering,2019,55(21):81-87.(in Chinese)
-
[4] 李炎,董庆兵,罗振涛,等.考虑表面形貌的接触应力分析[J].表面技术,2021,50(12):294-302.LI Yan,DONG Qingbing,LUO Zhentao,et al.Analysis of stress fields at line contact with consideration of surface topographies[J].Surface Technology,2019,50(12):294-302.(in Chinese)
-
[5] 王悦昶,刘莹,李鸿举.粗糙表面仿真方法综述[J].机械工程学报,2022,58(19):148-165.WANG Yuechang,LIU Ying,LI HongJu.A review of rough surface simulation methods[J].Journal of Mechanical Engineering,2022,58(19):148-165.(in Chinese)
-
[6] 闫铎,李磊涛,梁轩铭,等.粗糙表面接触的层级模型 [J].应用力学学报,2023,40(2):334-339.YAN Duo,LI Leitao,LIANG Xuanming,et al.A hierarchical contact model for rough surface[J].Chinese Journal of Applied Mechanics,2023,40(2):334-339.(in Chinese)
-
[7] JACKSON R L,GREEN I.A finite element study of elasto-plastic hemispherical contact against a rigid flat[J].Journal of Tribology,2005,127(2):343-354.
-
[8] LIU M,PROUDHON H.Finite element analysis of frictionless contact between a sinusoidal asperity and a rigid plane:elastic and initially plastic deformations[J].Mechanics of Materials,2014,77:125-141.
-
[9] MEGALINGAM A,RAMJI K S H.A complete single asperity-based statistical gaussian rough surface contact model[J].Journal of Bio-and Tribo-Corrosion,2020,6(4):1-16.
-
[10] LUAN B,ROBBINS M O.The breakdown of continuum models for mechanical contacts[J].Nature,2005,435(7044):929-932.
-
[11] LUAN B,ROBBINS M O.Contact of single asperities with varying adhesion:comparing continuum mechanics to atomistic simulations[J].Physical Review E,2006,74(2):026111.
-
[12] 雷海东,段芳莉,仇和兵,等.纳米级粗糙表面接触行为的分子动力学模拟[J].中国表面工程,2010,27(5):27-31.LEI Haidong,DUAN Fangli,QIU Heibing,et al.Molecular dynamics simulation of contact mechanics between nanoscale rough surfaces[J].China Surface Engineering,2010,27(5):27-31.(in Chinese)
-
[13] 林起崟,张瑜寒,洪军,等.晶粒尺寸对多晶铜接触力学特性的影响[J].中国机械工程,2021,32(19):2312-2320.LIN Qiyin,ZHANG Yuhan,HONG Jun,et al.Influences of grain sizes on contact mechanics properties of polycrystalline copper[J].China Mechanical Engineering,2021,32(19):2312-2320.(in Chinese)
-
[14] HE Y,SHE D S,LIU Z Y,et al.Atomistic observation on diffusion-mediated friction between single-asperity contacts[J].Nature Materials,2022,21(2):173-180.
-
[15] SI L,WANG X L,XIE G X,et al.Nano-adhesion and friction of multi-asperity contact:a molecular dynamics simulation study[J].Surface and Interface Analysis,2015,47(9):919-925.
-
[16] ZHENG X,ZHU H T,KIET TIEU A,et al.A molecular dynamics simulation of 3D rough lubricated contact[J].Tribology International,2013,67:217-221.
-
[17] ZHENG X,ZHU H T,KOSASIH B,et al.A molecular dynamics simulation of boundary lubrication:the effect of n-alkanes chain length and normal load[J].Wear,2013,301(1-2):62-69.
-
[18] 黄健萌,戴煜宸,林有希,等.纳观分形粗糙表面的建模分析[J].摩擦学学报,2018,38(2):138-144.HUANG Jianmeng,DAI Yuchen,LIN Youxi,et al.Modeling and analysis of fractal rough nanoscale surfaces[J].Tribology,2018,38(2):138-144.(in Chinese)
-
[19] DAI Y,LIN J,HUANG J M.Fractal contact behavior of single crystal copper substrate and rigid plane[J].Journal of Dispersion Science and Technology,2020,41(10):1504-1512.
-
[20] 黄仕平,吴杰,胡俊亮,等.基于分子动力学-格林函数法的微凸体接触数值分析[J].力学学报,2017,49(4):961-967.HUANG Shiping,WU Jie,HU Junliang,et al.Numerical analysis of asperity contact model based on molecular dynamics-green’s function method [J].Chinese Journal of Theoretical and Applied Mechanics,2017,49(4):961-967.(in Chinese)
-
[21] 黄仕平,陈枭,萧明强.基于分子动力学-格林函数法的分形粗糙表面摩擦行为研究[J].力学学报,2023,55(7):1484-1492.HUANG Shiping,CHEN Xiao,XIAO Mingqiang.Study on friction behavior of fractal rough surface based on molecular dynamics-green’s function method[J].Chinese Journal of Theoretical and Applied Mechanics,2023,55(7):1484-1492.(in Chinese)
-
[22] SPIJKER P,ANCIAUX G,MOLINARI J F.Dry sliding contact between rough surfaces at the atomistic scale[J].Tribology Letters,2011,44(2):279-285.
-
[23] SPIJKER P,ANCIAUX G,MOLINARI J F.The effect of loading on surface roughness at the atomistic level[J].Computational Mechanics,2012,50(3):273-283.
-
[24] 刘勇,夏天,陈志英,等.粗糙表面统计接触模型的提出与发展[J].摩擦学学报,2020,40(3):395-406.LIU Yong,XIA Tian,CHEN Zhiying,et al.Proposal and development of statistical contact model for rough surfaces [J].Tribology,2020,40(3):395-406.(in Chinese)
-
[25] PERSSON B N,ALBOHR O,TARTAGLINO U,et al.On the nature of surface roughness with application to contact mechanics,sealing,rubber friction and adhesion[J].Journal of Physics:Condensed Matter,2005,17(1):1-62.
-
[26] FOILES S M,BASKES M I,DAW M S.Embedded-atom-method functions for the fcc metals Cu,Ag,Au,Ni,Pd,Pt,and their alloys[J].Physical Review B,1986,33(12):7893-7991.
-
[27] TERSOFF J.Modeling solid-state chemistry:interatomic potentials for multicomponent systems[J].Physical Review B,1989,39(8):5566-5568.
-
[28] JONES J E.On the determination of molecular fields II from the equation of state of a gas[J].Proceedings of The Royal Society A:Mathematical,Physical and Engineering Sciences,1924,106(738):463-477.
-
[29] FILIPPOVA V P,KUNAVIN S A,PUGACHEV M S.Calculation of the parameters of the Lennard-Jones potential for pairs of identical atoms based on the properties of solid substances[J].Inorganic Materials:Applied Research,2015,6(1):1-4.
-
[30] MAYO S L,OLAFSON B D,GODDARD W A.DREIDING:a generic force field for molecular simulations[J].The Journal of Physical Chemistry,1990,94(26):8897-8909.
-
[31] RAPPÉ A C,CASEWIT C J,COLWELL K S,et al.UFF,a full periodic table force field for molecular mechanics and molecular dynamics simulations[J].Journal of The American Chemical Society 1992,25(114):10024-10035.
-
[32] SOLHJOO S,VAKIS A I.Surface roughness of gold substrates at the nanoscale:an atomistic simulation study[J].Tribology International,2017,115:165-178.
-
[33] WU B,SUN Y.Normal contact analysis between two self-affine fractal surfaces at the nanoscale by molecular dynamics simulations[J].Tribology Letters,2023,71(2):30-45.
-
[34] ZHENG X,ZHU H T,KOSASIH B,et al.Roughness and lubricant effect on 3D atomic asperity contact[J].Tribology Letters,2014,53:215-223.
-
[35] PERSSON B N J,Elastoplastic contact between randomly rough surfaces[J].Physical Review Letters,2001,87(11):116101.
-
[36] AKARAPU S,SHARP T,ROBBINS M O.Stiffness of contacts between rough surfaces[J].Physical Review Letters,2011,106(20):204301.
-
摘要
精密仪器的应用推动了机械零部件的纳米化,然而关于纳米级粗糙形貌与接触参量之间映射关系的研究有限,且不同外加负载下粗糙界面接触参量的动态变化特性尚未完全被揭示。采用分子动力学方法研究纳米级粗糙界面的法向接触特性。首先,通过对表面功率谱密度函数进行逆傅里叶变换构建随机粗糙表面,建立具有纳米级粗糙度的铜-金刚石界面法向接触分子动力学模型。然后,从原子尺度模拟纳米级粗糙界面的法向动态接触过程,分析纳米级粗糙界面在不同外加负载作用下的动态变化特性,包括法向接触力、实际接触面积、界面等效变形量等关键参量。最后,模拟不同粗糙度的界面法向接触过程,建立等效接触变形量与实际接触面积间的映射关系。纳米级粗糙界面法向接触特性研究表明:接触界面粗糙形貌恒定时,法向接触力、实际接触面积、接触变形量与外加负载呈正相关;相同外加负载时,表面粗糙度的增加会使实际接触原子数量减少,进而导致法向接触力、实际接触面积和界面等效变形量的减小;原子间相互作用力和原子扩散效应直接导致接触参量的动态变化受表面形貌影响;实际接触面积随界面等效变形量呈非线性增长,且两者间存在幂律映射关系。通过分子动力学模拟,揭示纳米级粗糙界面实际接触面积与等效变形量之间的函数关系,研究成果可为微纳尺度界面接触研究提供理论参考。
Abstract
The use of precision instruments facilitates the miniaturization of mechanical components, enhancing their efficiency and performance. Deformation at contact interfaces composed of mechanical components essentially derives from the interaction between nanosized asperities. Under external loading conditions, the presence of these nanosized asperities on rough interfaces can significantly reduce the actual contact area compared to the nominal area, leading to the localized stress concentration within the contact region. Similarly, contact parameters such as the normal contact force, contact pressure, and deformation directly impact the operational lifespan of mechanical components. Establishing an equivalent mechanical model for rough interfaces is a prerequisite to elucidate the underlying deformation mechanisms governing contact behaviors at the nanoscale. Therefore, understanding the normal contact behavior between nanoscale rough interfaces under various external loading conditions is crucial. At the nanoscale, the dispersion of atoms leads to the breakdown of the continuum mechanics theory. However, studies investigating the mapping relationship between the nanoscale roughness morphology and contact parameters are limited. In addition, very little information is available on the dynamic variations in the contact parameters of nanoscale rough interfaces under different applied loads. Furthermore, the application of the finite element method is restricted to microcontact processes and does not encompass contact analysis at the nanoscale. With advancements in computer technology, molecular dynamics has emerged as a widely employed approach for investigating nanoscale contact behaviors. The normal contact behaviors between nanoscale rough interfaces have been investigated through molecular dynamics simulations. First, random rough surfaces are constructed by applying an inverse Fourier transform to the surface power spectral density function, thereby establishing a molecular dynamics model for normal contact between nanoscale rough copper-diamond interfaces. Subsequently, the dynamic process of normal contact between nanoscale rough interfaces is simulated at an atomic scale. The dynamic variations in key parameters such as the normal contact force, actual contact area, and interface equivalent deformation are analyzed under various external loads. Finally, comprehensive simulations are conducted to study the normal contact process between nanoscale rough interfaces with varying surface roughness, inducing the establishment of a mapping relationship between the equivalent deformation and actual contact area. The results provide a qualitative understanding of the normal contact characteristics of nanoscale rough interfaces. The applied load shows a positive correlation with the normal contact force, actual contact area, and contact deformation when the surface roughness remains constant. This finding is consistent with the observed characteristics of interfaces featuring micron-scale roughness. Under identical loads, the surface roughness of the contact interfaces increases, resulting in reduced resistance to the deformation of nanosized asperities and facilitating deformation. This results in a decrease in the number of atoms in contact as well as a reduction in both the magnitude of the normal contact force and the size of the effective contact area. At the nanoscale, surface morphology significantly influences interatomic forces. As the contact interface becomes smoother, the interaction force between the atoms intensifies, leading to a wider fluctuation in the normal contact parameters such as the normal contact force and actual contact area. The actual contact area of the nanoscale rough interfaces exhibits a power-law mapping relationship with the equivalent deformation under external loading. Moreover, larger surface roughness leads to a smaller contact area. Normal contact analysis of nanoscale rough interfaces reveals variations in key parameters, including the normal contact force, actual contact area, and equivalent deformation under an external load. The establishment of a mapping relationship between the surface morphology and contact parameters not only offers a theoretical framework for investigating micro-nano scale contact behaviors but also provides invaluable support for enhancing the interface characteristics of precision instruments.